Ir al contenido principal

Blog 2do Periodo




Santiago Alejandro Moreno Cubillos



 Temas:
-Solucion de ecuaciones;Metodo de gauss jordan
-Cofactores 3x3
-Identidades Trigonometricas


Colegio:Leon Magno


Profesor:Luis Armero



 













Solucion de Ecuaciones por el metodo de gauss jordan:

En matematicas, la eliminación de Gauss-Jordan, llamada así debido a, carl gauss y Wilhem jordan, es un algoritmo del algebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuacion  tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.



Resultado de imagen para Solucion de Ecuaciones por el metodo de gauss jordan




Pasos para realizar ecuaciones:
  1. Ir a la columna no cero extrema izquierda
  2. Si la primera fila tiene un cero en esta columna, intercambiarlo con otra que no lo tenga.
  3. Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él.
  4. Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en forma escalonada).
  5. Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener un 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes.
Una variante interesante de la eliminación de Gauss es la que llamamos eliminación de Gauss-Jordan, (debido al mencionado Gauss y a Willhelm jordan), esta consiste en ir obteniendo los 1 delanteros durante los pasos uno al cuatro (llamados paso directo) así para cuando estos finalicen ya se obtendrá la matriz en forma escalonada reducida.


Cofactores 3x3


Dada una matriz cuadrada A, su matriz de adjuntos o matriz de cofactores cof(A) es la resultante de sustituir cada término  de A por el cofactor  de A. El término matriz adjunta adj(A) suele crear confusión, ya que en muchos tratados clásicos sobrealgebra lineal  corresponde a la matriz de cofactores traspuesta, sin embargo, en otros textos, se corresponde a la matriz de cofactores, puesto que llaman de la misma manera adjunto al cofactor y de ahí que sea adjunta Aparte, también se utiliza el símbolo  indistintamnte a cof para el cálculo en los elementos de una matriz, haciendo, si cabe, la confusión más amplia.

Matrices 3x3


Dada una matriz de 3 x 3:  

{\displaystyle \mathbf {A} ={\begin{pmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{pmatrix}}} 


 Su matriz de cofactores viene dada por:
{\displaystyle {\mbox{cof}}(\mathbf {A} )={\begin{pmatrix}+\left|{\begin{matrix}A_{22}&A_{23}\\A_{32}&A_{33}\end{matrix}}\right|&-\left|{\begin{matrix}A_{21}&A_{23}\\A_{31}&A_{33}\end{matrix}}\right|&+\left|{\begin{matrix}A_{21}&A_{22}\\A_{31}&A_{32}\end{matrix}}\right|\\&&\\-\left|{\begin{matrix}A_{12}&A_{13}\\A_{32}&A_{33}\end{matrix}}\right|&+\left|{\begin{matrix}A_{11}&A_{13}\\A_{31}&A_{33}\end{matrix}}\right|&-\left|{\begin{matrix}A_{11}&A_{12}\\A_{31}&A_{32}\end{matrix}}\right|\\&&\\+\left|{\begin{matrix}A_{12}&A_{13}\\A_{22}&A_{23}\end{matrix}}\right|&-\left|{\begin{matrix}A_{11}&A_{13}\\A_{21}&A_{23}\end{matrix}}\right|&+\left|{\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}}\right|\end{pmatrix}}={\begin{pmatrix}A_{22}A_{33}-A_{23}A_{32}&A_{23}A_{31}-A_{21}A_{33}&A_{21}A_{32}-A_{22}A_{31}\\A_{32}A_{13}-A_{33}A_{12}&A_{33}A_{11}-A_{31}A_{13}&A_{31}A_{12}-A_{32}A_{11}\\A_{12}A_{23}-A_{13}A_{22}&A_{13}A_{21}-A_{11}A_{23}&A_{11}A_{22}-A_{12}A_{21}\end{pmatrix}}} 

y por lo tanto la transpuesta de la matriz de cofactores es la matriz Adjunta:


{\displaystyle {\mbox{adj}}(\mathbf {A} )={\begin{pmatrix}+\left|{\begin{matrix}A_{22}&A_{23}\\A_{32}&A_{33}\end{matrix}}\right|&-\left|{\begin{matrix}A_{21}&A_{23}\\A_{31}&A_{33}\end{matrix}}\right|&+\left|{\begin{matrix}A_{21}&A_{22}\\A_{31}&A_{32}\end{matrix}}\right|\\&&\\-\left|{\begin{matrix}A_{12}&A_{13}\\A_{32}&A_{33}\end{matrix}}\right|&+\left|{\begin{matrix}A_{11}&A_{13}\\A_{31}&A_{33}\end{matrix}}\right|&-\left|{\begin{matrix}A_{11}&A_{12}\\A_{31}&A_{32}\end{matrix}}\right|\\&&\\+\left|{\begin{matrix}A_{12}&A_{13}\\A_{22}&A_{23}\end{matrix}}\right|&-\left|{\begin{matrix}A_{11}&A_{13}\\A_{21}&A_{23}\end{matrix}}\right|&+\left|{\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}}\right|\end{pmatrix}}^{T}}



Identidades Trigonometricas



Una identidad trigonométrica es una igualdad entre expresiones que contienenfunciones trigonometricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).


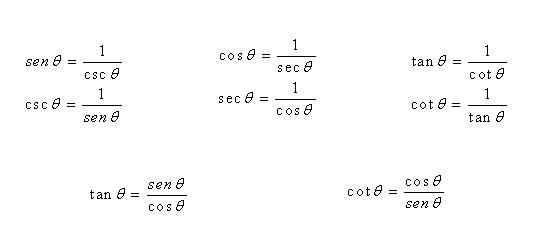
Resultado de imagen para identidades trigonometricas






















Comentarios

Publicar un comentario